Head of National Research Centre for Computer Animation
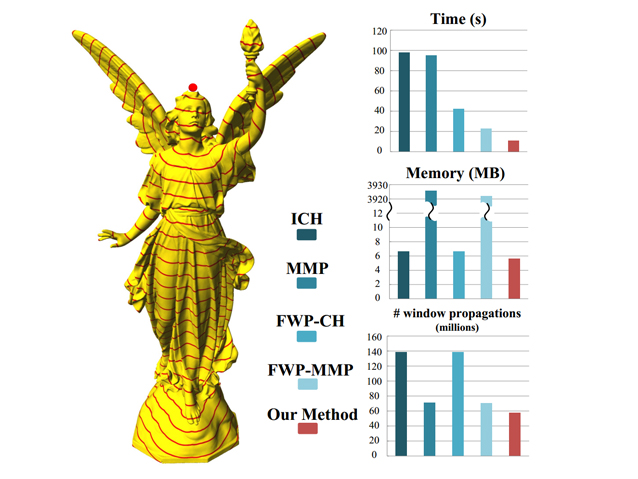
Computing discrete geodesic distance over triangle meshes is one of the fundamental problems in computational geometry and computer graphics. In this problem, an effective window pruning strategy can significantly affect the actual running time. Due to its importance, we conduct an in-depth study of window pruning operations in this paper, […]
Geodesic paths on surfaces are indispensable in many research and industrial areas, including architectural and aircraft design, human body animation, robotic path planning, terrain navigation, and reverse engineering. 3D models in these applications are typically large and complex. It is challenging for existing geodesic path algorithms to process large-scale models […]
Geodesic based Voronoi diagrams play an important role in many applications of computer graphics. Constructing such Voronoi diagrams usually resorts to exact geodesics. However, exact geodesic computation always consumes lots of time and memory, which has become the bottleneck of constructing geodesic based Voronoi diagrams. In this paper, we propose […]